儀器: BI-200SMNanoBrook 系列
摘要
動態光散射(DLS)是一種常用技術,用于測量可分散膠體顆粒以及其他納米材料的粒徑分布。與所有其他基于光散射的技術一樣,散射光的強度會明顯偏向較大的顆粒。在分析含有兩種或更多主要成分的樣品時,這一點必須予以考慮。假設兩種粒子數量相等且材質相同,那么較大的粒子總是會散射更多的光。因此,將光強加權視為原始分布加權是合理的。從光強加權轉換為體積加權、表面積加權或數量加權時必須格外謹慎,尤其是對于多峰粒徑分布的情況。使用得當的話,這種轉換能提供有關不同顆粒相對豐度的重要信息;但要是不加甄別地應用,則可能產生誤導。
引言
默認情況下,DLS 得到的是光強加權結果,其百分比強度與每個峰對總測量信號的貢獻直接相關。使用這種表示方式時,雙峰或多峰分布中的每個峰都以其對測量信號的總貢獻來表示。眾所周知,給定材料的散射光強會因顆粒大小而發生顯著變化,因此必須明白,兩個大小不等但強度相等的不同粒子群,其數量不可能相等 。
光散射中的主要光學對比度項源自樣品與溶劑之間的折射率差 Δn,光在顆粒與周圍溶劑的界面處發生散射,與在微觀表面散射的情況相同。除了這種對比度外,還有一個與尺寸或分子量相關的前置因子。
關鍵關系式為 I ∝d6
這個 d6 標量對大顆粒的散射光強有重大影響。當粒徑差異較小時,這種影響已經相當大;當有效粒徑差異超過一個數量級時,這種影響將變得極為突出,如下表所示。
| d,nm | d6 | Id/I20nm |
| 20 | 64,000,000 | 1 倍 |
| 40 | 4,096,000,000 | 64 倍 |
| 300 | 7.3X1014 | 11,390,625 倍 |
| 1000 | 1 X1018 | 15,625,000,000 倍 |
一個 40 nm 顆粒的散射光強是 20 nm 顆粒的 60 多倍;而一個 300 nm 顆粒的散射光強是 20 nm顆粒的 1100 萬倍以上。當粒徑跨度超過兩個數量級時,這種差異變得極其巨大。
幸運的是,基于數量濃度來制備樣本的情況相當少見,在多峰粒徑分布中,更常見的情形是區分質量濃度相等的顆粒群。由于較大的顆粒具有更高的分子量,這兩種效應通常會相互抵消。
例如,假設將兩種粒徑分別為 50 nm和 100 nm的銀納米顆粒混合,使兩者的最終濃度均為 1 mg/mL,那么將會有如下情況:
- 銀的密度 = 10.5 mg/cm3
- 濃度 1 = 濃度 2 = 1 mg/mL
- 直徑 1 = 50 nm,納米顆粒 1 濃度 = 1.5×10 15 particles/mL
- 直徑 2 = 100 nm,納米顆粒 2 濃度 = 1.2×10 14 particles/mL
- 顆粒體積 = 4/3π(0.5 x d)3
- 每顆粒質量 = ( 密度, mg/cm3) X ( 體積, cm3)
從上述例子可以看出,100 nm 顆粒的數量濃度比 50 nm 的低 8 倍。根據 d6 關系,我們知道每個100 nm 顆粒的散射光強是 50 nm 顆粒的 64倍,但當我們考慮數量濃度的差異時,會發現這種效應幾乎被抵消了。在假設質量相等的情況下,直徑增加兩倍,較大顆粒的信號凈增強僅為 8 倍。
二氧化硅顆粒懸浮液的制備:
制備幾種常見市售二氧化硅顆粒的混合物,包括LUDOX TM-50、AM-30 和市售低密度氣相二氧化硅。盡管表面化學和宏觀結構存在差異,但這三種材料都是二氧化硅,因此可以假設它們具有相似的的折射率。由于這三種顆粒的 Δn 相同,我們只需考慮由 d6 規則引起的對比度差異。
LUDOX TM-50 與 AM-30 混合物
[ TM-50 ]:2.5 mg/mL
標稱粒徑:22 nm
TM-50 的密度:1.4 g/cm3
[ AM-30 ]:1.5 mg/mL
標稱粒徑:12 nm
AM-30的密度:1.21 g/cm3
LUDOX TM-50 與氣相二氧化硅混合物
[ TM-50 ]:2 mg/mL
標稱粒徑:22 nm
TM-50的密度:1.4 g/cm3
[氣相二氧化硅]:0.2 mg/mL
標稱粒徑:0.2-0.3 μm
熔融石英的密度:0.037 g/cm3
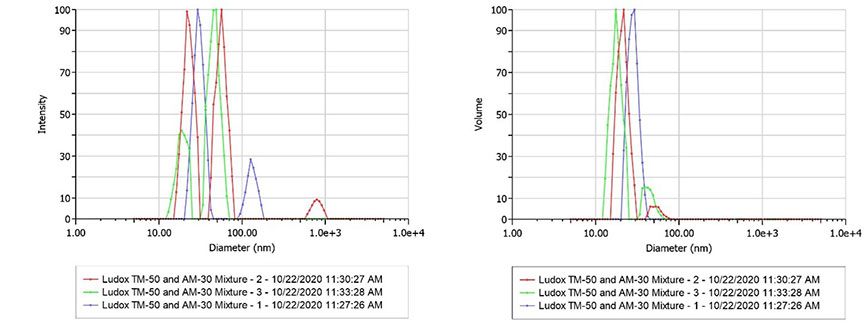
通過查看對 Ludox TM – 50 與 AM – 30 混合物的三次測量結果,可以在未經轉換的光強加權分布中(圖 1)清晰地識別出兩個顆粒群。我們還注意到,當采用體積加權時,兩個峰中較大的峰被抑制,從而突出了較大顆粒豐度較低這一情況。
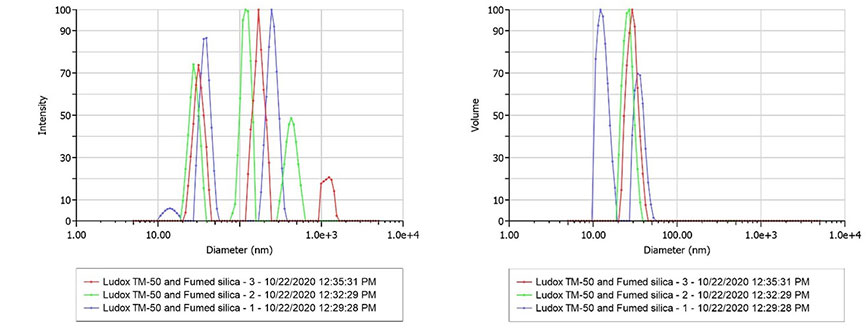
相比之下,當我們將 Ludox TM – 50 與氣相二氧化硅混合(圖 2)時,由于氣相二氧化硅的分形結構,它的顆粒形態遠沒有那么規整,盡管只有兩種成分存在,但分布卻顯得更加復雜。這個名義上的雙峰樣品在光強加權中呈現出一些低豐度的數據擬合偽影,分別位于在約 10 nm 和約 1000 nm 處。盡管這些偽影在光強加權分布中豐度較低(左圖),僅為實際測量信號中的次要成分,但當我們轉換為體積加權時(右圖),偽影被顯著放大。
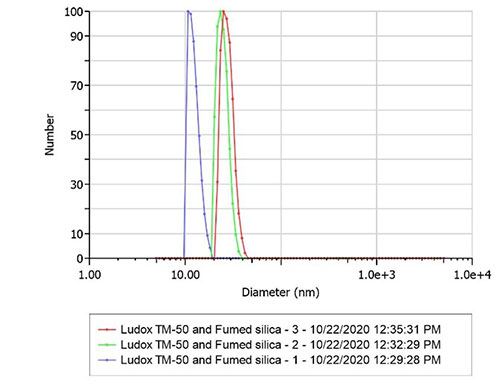
結論:
盲目地對多峰粒度分布進行重新歸一化存在風險,用戶最終可能會忽略最大組分的貢獻,同時過分強調較小的組分。顯然,當將 TM-50 與氣相二氧化硅混合時,這種效應在轉換為數量加權分布時進一步加劇(圖3),在三次測量的第一次測量中,它似乎成為唯一的峰,盡管它并不代表混合物中存在的任何一種顆粒。在極端情況下,這甚至可能意味著強調不存在的組分。
總結:
- 轉換為數量加權或體積加權時需格外謹慎。
- 在分析大量短時間 DLS 測量時,過度擬合可能會得到錯誤的粒徑分布結果。
- 很難通過 DLS 分辨出三個不同的顆粒群。
- 由于存在 d6 關系,光強加權分布在小粒徑處的噪聲信號將在數量、體積或表面積加權分布中占主導地位。
